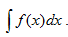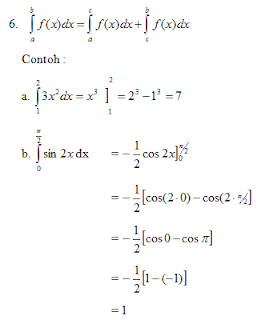Transformasi Geometri

Transformasi merupakan suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. Jenis-jenis dari transformasi yang dapat dilakukan antara lain :

1. Translasi (Pergeseran)
2. Refleksi(Pencerminan)
3. Rotasi(Perputaran)
4. Dilatasi(Penskalaan)

Berikut ini ilustrasinya :

TRANSLASI / PERGESERAN

Berdasarkan gambar di atas, segitiga ABC yang mempunyai koordinat A(3, 9), B(3, 3), C(6, 3) ditranslasikan:

Berdasarkan penjelasan diatas, maka untuk mencari nilai translasi dapat digunakan rumus sebagai berikut :

dimana :

• a menyatakan pergeseran horizontal (kekanan+, kekiri-)
• b menyatakan pergeseran vertikal (keatas+,kebawah-)

REFLEKSI / PENCERMINAN

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dicerminkan:

• terhadap sumbu Y menjadi segitiga A2B2C2 dengan koordinat A2(-3, 9), B2(-3, 3), C2(-6, 3)
• terhadap sumbu X menjadi segitiga A3B3C3 dengan koordinat A3(3, -9), B3(3, -3), C3(6, -3)
• terhadap titik (0, 0) menjadi segitiga A4B4C4 dengan koordinat A4(-3, -9), B4(-3, -3), C4(-6, -3)

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dicerminkan:

• terhadap garis x = -2 menjadi segitiga A5B5C5 dengan koordinat A5(-7, 9), B5(-7, 3), C5(-10, 3)
• terhadap sumbu y = 1 menjadi segitiga A6B6C6 dengan koordinat A6(3, -7), B6(3, -1), C6(6, -1)

Segitiga PQR dengan koordinat P(6, 4), Q(6, 1), R(10, 1) dicerminkan:

• terhadap garis y = x menjadi segitiga P2Q2R2 dengan koordinat P2(4, 6), Q2(1, 6), R2(1, 10)
• terhadap garis y = -x menjadi segitiga P3Q3R3 dengan koordinat P3(-4, -6), Q3(-1, -6), R3(-1, -10)

Berdasarkan penjelasan diatas dapat dirumuskan :

Pencerminan terhadap garis x = a atau y = b

Pencerminan terhadap sumbu x atau sumbu y

Pencerminan terhadap titik (0, 0)

Pencerminan terhadap garis y = x atau y = –x

Pencerminan terhadap garis y = mx + c

Jika m = tan θ maka:

ROTASI / PERPUTARAN

Untuk rotasi searah jarum jam, sudut diberi tanda negatif (–)

Untuk rotasi berlawanan arah jarum jam, sudut diberi tanda positif (+)

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dirotasi:

• +90° atau –270°  dengan pusat rotasi O(0, 0) menjadi segitiga A2B2C2 dengan koordinat A2(-9, 3), B2(-3, 3), C2(-3, 6)
• +270° atau –90°  dengan pusat rotasi O(0, 0) menjadi segitiga A3B3C3 dengan koordinat A2(9, -3), B2(3, -3), C2(3, -6)
• +180° atau –180° dengan pusat rotasi O(0, 0) menjadi segitiga A4B4C4 dengan koordinat A4(-3, -9), B4(-3, -3), C4(-6, -3)

Berdasarkan penjelasan diatas, maka rotasi dapat dirumuskan sebagai berikut :

Rotasi sejauh θ dengan pusat (a, b)

Rumus praktis untuk rotasi dengan pusat rotasi O(0, 0):

DILATASI / PENSKALAAN

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) didilatasi:

• dengan faktor skala k = 1/3 dan pusat dilatasi O(0, 0) menjadi segitiga A2B2C2 dengan koordinat A2(1, 3), B2(1, 1), C2(2, 1)
• dengan faktor skala k = 2 dan pusat dilatasi O(0, 0) menjadi segitiga A3B3C3 dengan koordinat A3(6, 18), B3(6, 6), C3(12, 6)

Untuk nilai k negatif, arah bayangan berlawanan dengan arah aslinya.

Berdasarkan penjelasan diatas, maka dapat dirumuskan :

Dilatasi dengan pusat (a, b) dan faktor skala k

Rumus praktis dilatasi dengan faktor skala k dan pusat dilatasi O(0, 0):

Selain 4 transformasi yang telah dijelaskan diatas, juga terdapat 2 transformasi lagi yaitu shearing / gusuran dan stretching / regangan. Perhatikan penjelasan dibawah ini :

GUSURAN/SHEARING

Persegi panjang ABCD dengan koordinat A(1, 1), B(4, 1), C(4, 6), D(1, 6) akan digusur:

• menurut arah sumbu X (invariant sumbu X) dengan faktor skala k = 2 menjadi persegi panjang A2B2C2D2 dengan koordinat A2(3, 1), B2(6, 1), C2(16, 6), D2(13, 6)
• menurut arah sumbu Y (invariant sumbu Y) dengan faktor skala k = 2 menjadi persegi panjang A3B3C3D3 dengan koordinat A3(1, 3), B3(4, 9), C3(4, 14), D3(1, 8)

Pengaruh nilai k:

• untuk gusuran menurut arah sumbu X → k positif arahnya ke kanan, k negatif arahnya ke kiri
• untuk gusuran menurut arah sumbu Y → k positif arahnya ke atas, k negatif arahnya ke bawah

Berdasarkan penjelasan diatas, maka dapat dirumuskan sebagai berikut :

Gusuran menurut arah sumbu X (Gx) dengan faktor skala k maka :

Gusuran menurut arah sumbu Y (Gy) dengan faktor skala k maka :

STRETCHING / REGANGAN

Persegi panjang ABCD dengan koordinat A(1, 1), B(4, 1), C(4, 6), D(1, 6) diregangkan:

• searah sumbu X dengan faktor skala k = 3 menjadi A2B2C2D2 dengan koordinat A2(3, 1), B2(12, 1), C2(12, 6), D2(3, 6)
• searah sumbu Y dengan faktor skala k = 2 menjadi A3B3C3D3 dengan koordinat A3(1, 2), B3(4, 2), C3(4, 12), D3(1, 12)

Pengaruh nilai k:

• untuk regangan searah sumbu X → k positif arahnya ke kanan, k negatif arahnya ke kiri
• untuk regangan searah sumbu Y → k positif arahnya ke atas, k negatif arahnya ke bawah

Berdasarkan penjelasan diatas, maka dapat dirumuskan :

Regangan searah sumbu X (Sx) dengan faktor skala k

Regangan searah sumbu Y (Sy) dengan faktor skala k

Transformasi dengan Matriks Transformasi Tertentu

KOMPOSISI TRANSFORMASI

merupakan gabungan dari beberapa transformasi. Misalnya kita mempunyai transformasi T1 akan dilanjutkan ke T2 maka ditulis T2oT1.

Komposisi Khusus :

1. Dua pencerminan yang berurutan terhadap sumbu-sumbu yang sejajar

2. Dua pencerminan yang berurutan terhadap dua sumbu yang tegak lurus ekuivalen dengan rotasi 180º yang pusatnya adalah titik potong kedua sumbu tersebut.

3. Dua pencerminan terhadap dua sumbu yang berpotongan ekuivalen dengan rotasi dimana titik pusat adalah titik potong kedua sumbu dan sudutnya adalah sudut antara kedua sumbu.

4. Dua rotasi berurutan terhadap pusat yang sama ekuivalen dengan rotasi dimana pusatnya sejauh jumlah sudut keduanya.

LUAS HASIL TRANSFORMASI

Transformasi yang berupa translasi, refleksi, dan rotasi tidak mengubah luas suatu benda

Mencari luas segitiga ABC jika diketahui koordinat titik A, B, dan C nya, maka kita dapat gunakan rumus :

Perhatikan contoh soal transformasi berikut ini.

Tentukanlah persamaan bayangan kurva y = x2 + 3x -4 jika dicerminkan terhadap sumbu X, kemudian didilatasikan dengan faktor skala 2 dengan pusat dilatasi O(0, 0)

Penyelesaian :

cara 1 : cara langsung

cara 2 : menggunakan matriks

Menu Sarapan Sehat dan Praktis

Di pagi hari, banyak orang yang memilih melewatkan sarapan karena berdalih tak punya waktu. Padahal, sarapan memiliki banyak manfaat penting bagi tubuh. Salah satunya, sarapan membantu meningkatkan daya konsentrasi dalam bekerja dan belajar. Berikut ini 10 menu sarapan sehat yang dapat Anda siapkan tiap harinya dalam waktu kurang dari 10 menit

1. Telur orak-arik
Bahan: Telur; Sayur potong (wortel, jagung, atau jamur)
Waktu yang dibutuhkan: 5-8 menit

Source: food

Telur orak-arik atau yang juga dikenal dengan nama scrambled egg ini merupakan menu sarapan yang amat praktis, namun tetap bergizi. Sebagai variasi, Anda bisa menambahkan sayuran, seperti wortel, jagung, atau jamur ke dalamnya. Keju parut pun akan menambah kelezatan menu yang satu ini. Jika Anda ingin lebih kenyang, cukup selipkan telur orak-arik di tengah roti tawar. Praktis, bukan?

2. Sereal

Bahan: Sereal; Yogurt atau Susu; Buah-buahan

Waktu yang dibutuhkan: 3-5 menit

Source: flickr

Berbagai macam sereal sangat mudah ditemui di supermarket sehingga Anda tinggal memilih sereal apa yang paling disukai oleh keluarga. Penyajiannya yang mudah dan gizi yang cukup lengkap membuat sereal menjadi salah satu menu sarapan favorit keluarga. Jika selama ini Anda mencampur sereal dengan susu, cobalah menggantinya dengan yogurt. Tambahkan pula beberapa potong buah-buahan segar.

3. Buah dan keju

Bahan: Apel; Keju cheddar

Waktu yang dibutuhkan: 3-5 menit

Source: thecurvycarrot

Bagi Anda yang sedang menjalani program penurunan berat badan, menu ini sangat cocok bagi Anda. Cukup potong-potong buah favorit Anda, misalnya buah apel, dan sajikan bersama keju cheddar. Asupan vitamin dari buah dan kalori dari keju akan membuat Anda tetap fit menjalani aktivitas sepanjang hari.

4. Smoothies

Bahan: Buah-buahan (seperti apel, pisang, dan stroberi); Susu rendah lemak; Oatmeal

Waktu yang dibutuhkan: 5-10 menit

Source: foodopia

Jika Anda mempunyai segudang kesibukan di pagi hari, smoothies bisa menyelamatkan nutrisi sarapan Anda. Sebab, smoothies bisa disiapkan dalam hitungan menit saja. Smoothies yang paling cocok untuk menu sarapan adalah perpaduan pisang dengan stroberi yang diblender dengan susu rendah lemak. Untuk membuat smoothies yang lebih mengenyangkan, Anda bisa menambahkan oatmeal atau buah beku ke dalamnya. Menu sarapan yang satu ini pun bisa Anda nikmati di mana saja.

5. Roti bakar

Bahan: Roti; Selai

Waktu yang dibutuhkan: 3-5 menit

Source: brownbutterfield

Menu sarapan yang satu ini sangat populer, terutama di negara Barat. Hal ini tak mengherankan karena kandungan gizi yang terkandung dalam roti dan selai mampu menjaga aktifitas Anda sepanjang hari. Biasanya, roti bakar dibuat dengan mesin toaster. Namun, jangan khawatir jika Anda tidak memiliki toaster. Manfaatkan teflon yang telah diolesi dengan sedikit margarin untuk membuat roti bakar lezat versi Anda.

6. Pancake

Bahan: Tepung terigu; Telur; Susu cair; Margarin; Sirup gula atau Madu

Waktu yang dibutuhkan: 4-8 menit

Source: juzkiryoma

Membuat pancake ternyata sangat mudah. Anda hanya perlu menyiapkan tepung terigu, telur, susu cair, dan margarin. Campurkan semua bahan itu, kemudian masak di teflon agar tak lengket. Sajikan bersama sirup gula atau madu. Jika ingin sedikit bereksperimen, Anda bisa menambahkan potongan buah dan beberapa scoop eskrim di atasnya. Selain lezat dan bergizi, menu yang satu ini pun akan mengenyangkan Anda dan keluarga.

7. Sandwich

Bahan: Roti tawar; Sayur; Keju; Telur; Daging asap

Waktu yang dibutuhkan: 5-10 menit

Source: eggplantandcheese

Menu sarapan yang satu ini pasti sudah familiar bagi Anda. Sandwich memang populer disantap ketika sarapan karena kandungan gizinya yang cukup lengkap dari sayur, keju, telur, dan daging asap. Sandwich juga dapat Anda bawa sebagai bekal makan siang yang amat praktis.

8. Onigiri

Bahan: Nasi putih; Lembaran rumput laut

Waktu yang dibutuhkan: 4-8 menit

Source: bananagranola

Kebanyakan orang Indonesia merasa tidak lengkap bila tak memasukkan nasi ke dalam menu makanan, termasuk ketika sarapan. Jika Anda merasa demikian, menyantap onigiri saat sarapan bisa jadi menu favorit Anda. Tak perlu waktu lama untuk menyiapkan onigiri, terutama jika Anda sudah memiliki persediaan nasi. Cukup membentuk bulatan dengan nasi, mengisinya dengan isian sesuai selera, lalu memberi nori atau lembaran rumput laut sebagai pengikatnya. Serunya lagi, Anda bisa berkreasi dengan isian onigiri; mulai dari daging ayam, telur, abon, atau hanya garam.

9. Salad buah

Bahan: Buah-buahan

Waktu yang diperlukan: 3-5 menit

Source: theroastedroot

Menu yang satu ini bisa Anda buat sekaligus dalam porsi besar, lalu disimpan di kulkas untuk sarapan berikutnya. Sangat efisien, bukan? Menyajikan salad buah pun tak membutuhkan waktu lama karena Anda hanya perlu mencampurkan potongan buah favorit Anda dengan yoghurt, susu kental manis atau madu, dan sedikit perasan jeruk lemon. Tak perlu ragu dengan kandungan gizi yang terkandung dalam menu ini karena vitamin dalam buah-buahan pasti sangat menyehatkan.

10. Oatmeal

Bahan: Oatmeal; Madu; Buah-buahan

Waktu yang diperlukan: 3-6 menit

Source: royalfood

Penyajian oatmeal hampir sama dengan sereal. Bedanya, ada jenis oatmeal tertentu yang harus dimasak. Untuk menghemat waktu, pilihlah oatmeal yang hanya perlu diseduh dengan air panas. Sayangnya, di Indonesia oatmeal belum populer karena rasanya yang hambar. Padahal, kandungan serat yang terkandung di dalamnya sangat tinggi. Untuk itu, Anda bisa menambahkan madu dan potongan buah untuk rasa yang lebih mengundang selera.

kalkulus : Intergral

1.1 Definisi Integral Tak Tentu (Indefinite Integral)

Jika maka y adalah fungsi yang mempunyai turunan f(x) dan disebut anti turunan

(antiderivate) dari f(x) atau integral tak tentu dari f(x)yang diberi notasi . Sebaliknya, jika

karena turunan dari suatu konstanta adalah nol, maka suatu integral tak tentu

mempunyai suku konstanta sembarang.

1.2 Rumus-rumus Integral Tak Tentu

1.3 Definisi Integral Tentu

Andaikan f(x) didefinisikan dalam selang Selang ini dibagi menjadi n bagian yang sama

panjang, yaitu . Maka integral tentu dari f(x) antara x = a dan x =b didefinisikan

sebagai berikut:

Limit ini pasti ada jika f(x) kontinu sepotong demi sepotong jika

maka menurut dalil pokok dari kalkulus integral, integral tentu diatas dapat dihitung dengan

rumus :

1.4 Rumus-rumus Integral tentu

dengan k sebagai konstanta sembarang.



1.5 Integral Parsial
Prinsip dasar integral parsial :

1. Salah satunya dimisalkan U
2. Sisinya yang lain (termasuk dx) dianggap sebagai dv

Sehingga bentuk integral parsial adalah sebagai berikut :

1.1 Beberapa Aplikasi dari Integral

a. Perhitungan Luas suatu kurva terhadap sumbu x





b. Menghitung luas diantara dua buah kurva

c. Menghitung volume benda putar yang diputar terhadap sumbu koordinat