Kalkulus

I PENDAHULUAN

0.1 Bilangan Real, Estimasi, dan Logika
Dasar dan kalkulus adalah sistem bilangan real dan sifat-sifatnya. Tetapi. apakah bilangan real itu dan apa sifat-sifatnya?
Bilangan BuIat dan Rasional Bilangan paling sederhana di antara semuanya adalah bilangan asli (natural number)
.1. 2.3.4.5.6,
ngan bilangan asli kita dapat menghitung: bilangan bulat (integer)
—3. —2. —1, 0. 1. 2. 3



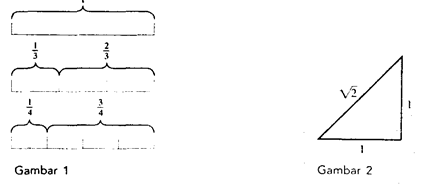
Bilangan yang dapat dituliskan dalam bentuk m/n, dengan m dan n bilangan bulat serta n ≠ 0, disebut bilangan rasional.
√2 tidak dapat dituliskan sebagai hasil-bagi dan dua bilangan bulat Jadi √2 adalah bilangan irasional (bukan rasional).
Bilangan Real Tinjaulah semua bilangan (rasional dan irasional) yang dapat mengukur panjang, beserta negatif dari bilangan-bilangan tersebut dan nol. Bilangan-bilangan ini disebut sebagai bilangan real.

 
Desimal Berulang dan Tak berulang  Setiap bilangan rasional dapat dituliskan sebagai desimal, karena sesuai definisi bilangan rasional selalu dapat dinyatakan sebagai hasil-bagi dua bilangan bulat; jika kita membagi pembilang dengan penyebut. kita memperoleh desimal (Gambar 5). Sebagai contoh,
1/2 = 0,5      3/8 = 0,375      3/7  = 0,428571428571428571
Bilangan irasional juga dapat dinyatakan sebagai desimal. Sebagai contoh.
√2 = 1.4142135623 ..., π = 3.1415926535


 
0.2  Pertidaksamaan dan Nilai Mutlak


Nilai mutlak adalah suatu bilangan real x dinyatakan oleh lxl, didefinisikan sebagai
| x | = x jika x≥0
| x | = -x jika x<0
    sifat-sifat nilai mutlak adalah tidak menimbulkan masalah dalam proses perkalian dan pembagian tapi begitu dalam proses penambahan dan pengurangan.
    | ab |= | a |  | b |〖^〗
    |a/b| = (|a|)/(|b|)
    | a+b | ≤ | a | + | b | (pertidaksamaan segitiga)
    | a-b || ≤ || a | - | b ||
pertidaksamaan yang melibatkan nilai mutlak
    |x| < a  - a < x < a
    |x| > a  x < - a / x > a



0.3 Sistem Koordinat Rektanguler
Persamaan iingkaran Dari rumus jarak ke persamaan suatu lingkaran hanyalah sebuah Iangkah kecil. Lingkaran adalah himpunan titik-titik yang terletak pada suatu jarak tetap (jari-jari) dari suatu titik tetap (pusat). Misalkan (x, y) menyatakan titik sebarang pada lingkaran ini. Menurut Rumus Jarak

 
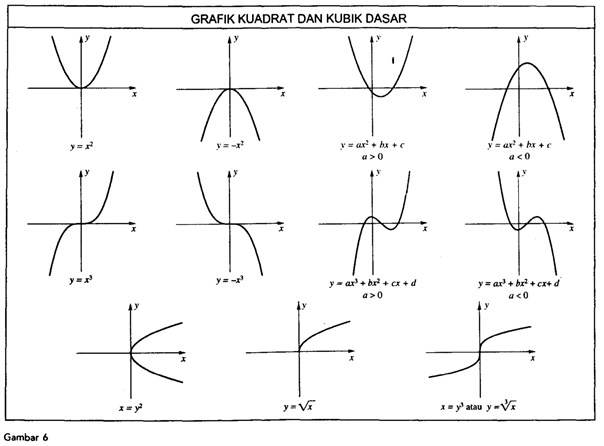
0.4 Grafik Persamaan
Grafik suatu persamaan dalam x dan y terdiri atas titik-titik di bidang yang koordinat-koordinat (x,y)-nya memenuhi persamaan yakni, membuat suatu identitas yang benar.
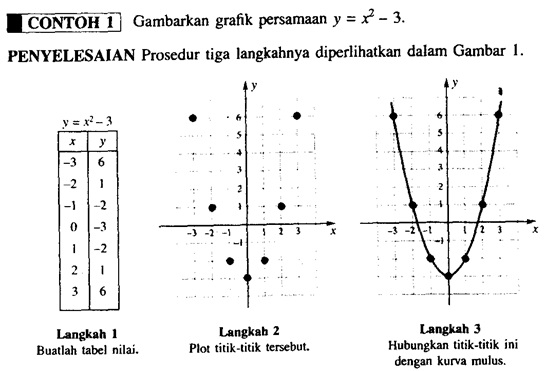
Prosedur Penggambaran Grafik Untuk menggambarkan suatu persamaan, misalnya y = 〖2x〗^3 - x + 19, kita dapat mengikuti prosedur tiga langkah sederhana:
Langkah 1: Dapatkan koordinat-koordinat beberapa titik yang memenuhi persamaan.
Langkah 2: Plotlah titik-titik tersebut pada bidang.
Langkah 3: Hubungkan titik-titik tersebut dengan sebuah kurva mulus.  








0.5 Fungsi dan Grafiknya
Definisi   
sebuah fungsi f adaIah suatu aturan korespondensi yang menghubungkan tiap obyek x dalam satu himpunan, yang disebut daerah asal (domain), dengan sebuah nilai tunggal f(x) dari suatu himpunan kedua. Himpunan nilal yang diperoleh secara
demikian disebut daerah hasil (range) fungsi.


Daerah asal dan daerah hasil untuk fungsi f dan g, diperlihatkan dalam tabel berikut.




0.6. Operasi pada Fungsi



Dengan asumsi bahwa f dan g mempunyai daerah asal alami, kita akan memperoleh:

0.7 Fungsi Trigonometri
Definisi Fungsi sinus dan kosinus
Misalkan t bilangan real yang menentukan titik P(x, y) seperti ditunjukkan di atas.
Maka
        sin t = y    dan    cos t = x







BAB II LIMIT




1.1 Pendahuluan limit




1.2 Pengkajian Mendalam tentang Limit






1.3 Teorema Limit












1.4 Limit Melibatkan ungsi Trigonometri




1.5 Limit di Tak-hingga dan Limit Tak-berhingga

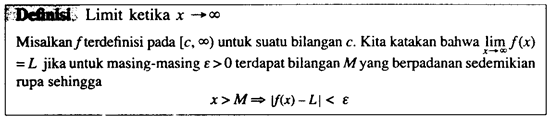
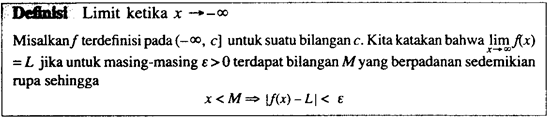
1.6 Kontinuitas Fungsi




Teorema A



Teorema D








BAB III TURUNAN


2.1 Dua Masalah dengan Satu Tema

2.2 Turunan

Jika limit ini memang ada, dikatakan bahwa f terdiferensiasi di c. Pencarian turunandisebut diferensiasi, bagian kalkulus yang berhubungan dengan turunan disebut kalkulusdiferensial.

Ø  Bentuk-bentuk Setara untuk Turunan Tidak ada yang keramat tentang penggunaaahuruf h datam mendefinisikan f(c). Misalkan, perhatikan bahwa

Ø  Keterdiferensiasian Mengimplikasikan Kontinuitas Jika sebuah kurva mempunyai sebuah garis singgung di sebuah titik. maka kurva itu tidak dapat melompat atau sangat berayun di titik tersebut. Perumusan yang presisi dari fakta ini merupakan sebuah teorema penting.

2.3 Aturan Pencarian Turunan

Aturan Konstanta dan Pangkat Grafik fungsi konstanta f(x) = k adalah sebuahgaris mendatar. yang karenanya mempunyai kemiringan nol di mana-mana.ini merupakan suatu cara untuk memahami teorema pertama kita.

2.4 Turunan Fungsi Trigonometri

2.5 Aturan Rantai

2.6 Turunan Tingkat Tinggi

Operasi diferensiasi mengambil sebuah fungsi f dan menghasilkan sebuah fungsi baru f. Jika f’ sekarang kita difereniasikan, kita masih tetap menghasilkan fungsi lain, dinyatakan oleh f (dibaca “f dua aksen”) dan disebut turunan kedua dari f. Pada gilirannya dia boleh didiferensiasikan lagi. dengan demikian menghasilkan f’. yang disebut turunan ketiga dari f. Turunan keempat dinyatakan turunan kelima dinyatakan dan seterusnya.

2.7 Diferensiasi Implisit

Bukti Karena r rasional, maka r dapat dituliskan sebagai p/q, di mana p dan q bilangan

bulat dan q > 0. Misalkan

2.8 Laju Yang Berkaitan

Masalah Laju yang Berhubungan dengan Grafik Seringkali dalam situasi kehidupan nyata, kita tidak mengetahui rumus untuk suatu fungsi tertentu, tetapi hanya mempunyai grafik yang ditentukan secara empinis.

2.9 Diferensial dan Aprosimasi

BAB IV

3.1 Maksimum dan Minimum

3.2 Kemonotonan dan Kecekungan

3.3 Ekstrim Lokal dan Ekstrim pada Interval Terbuka

3.4 Soal-Soal Praktis

Berdasarkan pada contoh dan teori yang dikembangkan dalam tiga subbab pertama dari bab ini, kami menyarankan metode langkah demi langkah berikut yang dapat diterapkan dalam banyak optimisasi praktis.

Langkah 1: Buat sebuah gambar untuk masalah dan berikan variabel-variabel yang sesuai   untuk besaran-besaran penting.                                                                              Langkah 2: Tuliskan rumus untuk fungsi tujuan Q yang harus dimaksimumkan (diminimumkan) dalam bentuk variabel-variabel dan langkah 1.                              Langkah 3: Gunakan kondisi-kondisi masalah untuk menghilangkan semua kecuali satu dari variabel-variabel ini dan karenanya menyatakan Q sebagai fungsi dan variabel tunggal. Langkah 4: Carilah titik-titik kritis (titik ujung, titik stasioner. tilik singular)             Langkah 5: Substitusikan nilai-nilai kritis ke dalam fungsi tujuan atau gunakan teori dari subbab terakhir (yaitu Uji Turunan Pertama dan Kedua) untuk menentukan maksimum atau minimum.

 

3.5 Penggambaran Grafik Fungsi Menggunakan Kalkulus

Ringkasan Metode. Dalam menggambarkan grafik fungsi, tidak terdapat pengganti untuk akal sehat. Tetapi. dalam banyak hal prosedur berikut akan sangat membantu.

Langkah 1: Analisis prakalkulus.

(a) Periksa daerah asal dan daerah hasil fungsi untuk melihat apakah ada daerah di bidang yang dikecualikan.

(b) Uji kesinietrian terhadap sumbu-y dan titik asal. (Apakah fungsi genap atau ganjil).

(c) Cari perpotongan dengan sumbu-sumbu koordinat.

L.angkah 2: Analisis kalkulus.

(a) Gunakan turunan pertama untuk mencari titik-titik kritis dan mengetahui tempat-tempat grafik menaik dan menurun.

(b) Uji titik-titik kritis untuk maksimum dan minimum lokal.

(c) Gunakan turunan kedua untuk mengetahui tempat-tempat grafik cekung ke atas dan cekung ke bawah dan untuk melokasikan titik balik.

(d) Cari asimtot-asimtot.

Langkah 3: Gambarkan beberapa titik (termasuk semua titik kritis dan titik belok).

Langkah 4: Sketsakan grafik.